hackpark2022_shiftycode

rev

周末做的一个很有趣的逆向，但是没在比赛结束之前做出来。第一次做VM的逆向，也算是打消了对未知的恐惧。感觉还是挺有意思的。

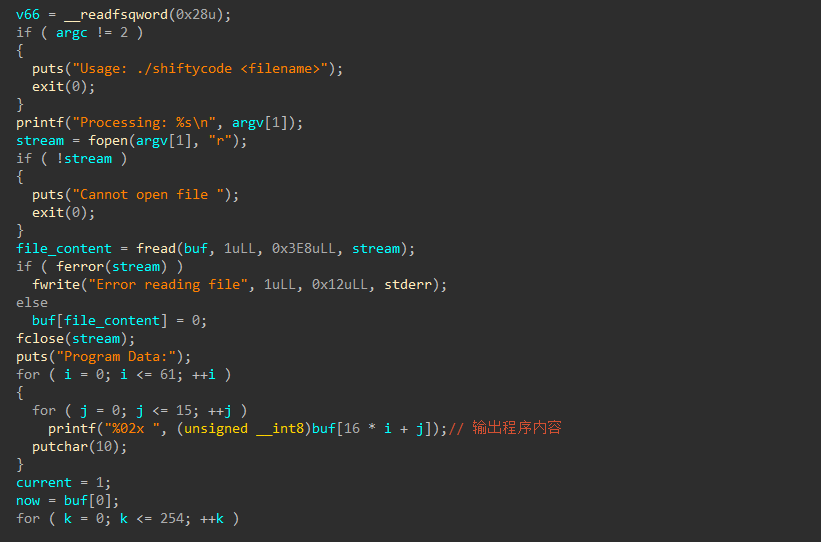
简单逆向

题目是shiftycode，VM的源码也十分简单。主要逻辑全部在main函数中。

文件首先接受一个bytecode，这个字节码题目也给了，其中就包含了检验flag的逻辑。

输出

我们直接运行

1
./shiftycode ./bin

程序会给我们输出很多字节码。逻辑如下。这也就方便我们观察字节码是什么。

image-20220415162712847

接着就到了循环。其实很好逆向，就是一个循环，类似switch-case语句，不断读取字节码，识别字节码的指令，然后根据指令做相应的事情。

image-20220415162756221

这里可以看到shiftycode的含义了。可以看到在每一次判断oprand之后，都会对当前的oprand自增。这样相当于下一次调用相同指令的code不一样。(如上面的++add)。

同时,在add中，如果第二个操作数是1和2，对应的行为也有差别

其余的逻辑很简单。这里举一个例子说明。其他的结构大同小异。

例如字节码

04 02 21 05

就可以被翻译为 all[0x21] += all[5]。注意第二个字节这里如果是01，就表示第四个字节是一个立即数，如果是02就表示操作数是我们输入的下表为5的位置。其余的还有一些跳转指令、比较指令、加减乘除都有。

整体逻辑

经过对bytecode的分析，可以大致总结出本题的逻辑。字节码和对应的汇编指令就写在下面了。注意这道题有一些跳转，一开始并不知道是否需要跳转，但是可以看到这些跳转大都是连续的(也就是说一个跳转的下一跳，还是一个跳转。这样最终将越过所有的检验逻辑)因此我最后尝试所有的跳转都无法进行，可以得到结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
// 接受用户输入[0,0x25]个字符
06 00 07 01 08 02 09 03 0a 04 0b 05 0c 06 0d 07 
0e 08 0f 09 10 0a 11 0b 12 0c 13 0d 14 0e 15 0f 
16 10 17 11 18 12 19 13 1a 14 1b 15 1c 16 1d 17 
1e 18 1f 19 20 1a 21 ff 22 ff 23 ff 24 ff 25 ff 
26 ff 27 ff 28 ff 29 ff 2a ff 2b ff 2c ff 2d ff

// all即为用户输入所储存的地方
// cmd是当前指令指针位置
07 01 00 66 ;if all[0] !=’f'
05 01 04 ; cmd+4 
08 03 01 6d ;if all[1] >='k'
06 01 04 ; cmd+4
09 04 01 6b ;if all[1] <='m'
07 01 18 ; cmd+0x18 


// x
00 02 1e 02 ; all[0x1e] +=all[2]
01 02 1f 03 ; all[0x1f] +=all[3]
02 02 20 03 ; all[0x20] +=all[3]
03 02 1f 1e ; all[0x1f] +=all[0x1e]
01 02 20 1e ; all[0x20] -=all[0x1e]


0a 01 1f c8  ; if all[0x1f] !=0xc8 
08 01 08 ; cmd+=8 
02 02 1f 20 ; all[0x1f] -=all[0x20]
0b 01 1f c2 ; if all[0x1f]!=0xc2 
09 01 04 ; cmd +=4 
0c 01 04 7b ; if all[0x4] !='{'
0a 01 04 ; cmd+=4 
0d 01 1a 7d ; if all[0x1a] !='}'
0b 01 0c ; cmd+=0xc 


# 
04 02 21 05 ; all[0x21] += all[5]
05 02 21 07 ; all[0x21] += all[7]
0e 01 21 cc ; if all[0x21] !=0xcc
0c 01 10 ; cmd +=0x10 

06 02 21 06 ; all[0x21] += all[6]
07 02 22 21 ; all[0x22] += all[0x21]
03 01 22 64 ; all[0x22] -=0x64
0f 01 22 e1 ; if all[0x22] !=0xe1
0d 01 08 ; cmd +=0x8

04 02 21 05 ; all[0x21] -=all[0x5]

10 01 21 d8 ; if all[0x21] !=0xd8
0e 01 0c ;cmd +=0xc

08 02 23 09 ; all[0x23] +=all[0x9]
09 01 23 0b ; all[0x23] += 0xb
11 02 08 23 ; if all[0x8] != all[0x23]
0f 01 0c ; cmd +=0xc

0a 02 24 0a ; all[0x24] +=all[0xa]
0b 01 24 42 ; all[0x24] +=0x42
12 02 08 24 ; if all[0x8] != all[0x24]
10 01 10 ; cmd +=0x10

0c 02 25 0c ; all[0x25] +=all[0xc]
0d 02 25 0b ; all[0x25] +=all[0xb]
05 02 25 08 ; all[0x25] -=all[0x8]
13 01 25 67 ; if all[0x25] !=0x67
11 01 18 ;cmd +=0x18

0e 02 26 0c ; all[0x26] +=all[0xc]
0f 02 26 0a ; all[0x26] +=all[0xa]
06 02 26 09 ; all[0x26] -=all[0x9]
10 02 27 0b ; all[0x27] +=all[0xb]
07 01 27 29 ; all[0x27] -=0x29
14 02 26 27 ; if all[0x26] !=all[0x27]
12 01 f3 ; cmd +=0xf3

11 01 27 29 ; all[0x27] +=0x29
08 02 27 0a ; all[0x27] -=all[0xa]
15 01 27 35 ; if all[0x27] !=0x35
13 01 e4 ; cmd +=0xe4

16 02 0e 13 ; if all[0xe] != all[0x13]
14 01 dd ; cmd +=0xdd

17 02 0f 12 ; if all[0xf] != all[0x12]
15 01 d6 ; cmd +=0xd6

18 02 10 07 ; if all[0x10] != all[0x7]
16 01 cf ; cmd +=0xcf

12 02 28 0d ; all[0x28] +=all[0xd]
09 02 28 12 ; all[0x28] -=all[0x12]
0a 02 28 11 ; all[0x28] -=all[0x11]
19 01 28 00 ; if all[0x28] != 0
17 01 bc ; cmd +=0xbc

1a 05 11 12 ; if all[0x11] >= all[0x12]
18 01 b5 ; cmd +=0xb5

1b 06 11 13 ; if all[0x11] <=all[0x13]
19 01 ae ; cmd +=0xae

13 02 28 12 ; all[0x28] +=all[0x12]
0b 02 28 13 ; all[0x28] -=all[0x13]
1c 01 28 02 ; if all[0x28] !=0x2
1a 01 9f ; cmd+=0x9f

14 02 29 0d ; all[0x29] +=all[0xd]
0c 01 29 36 ; all[0x29] -=0x36
1d 02 29 0e ; if all[0x29] !=all[0x0e]
1b 01 90 ; cmd +=0x90

15 02 2a 13 ; all[0x2a] += all[0x13]
02 01 2a 02 ; all[0x2a] *= 0x2
1e 02 2a 17 ; if all[0x2a] != all[0x17]
1c 01 81 ; cmd +=0x81

1f 02 14 10 ; if all[0x14] != all[0x10]
1d 01 7a ; cmd +=0x7a

20 02 16 0a ; if all[0x16] != all[0x0a]
1e 01 73 ; cmd +=0x73

16 02 2b 15 ; all[0x2b] +=all[0x15]
03 01 2a 02 ; all[0x2a] *=0x2 ==> no use!
03 01 2b 02 ; all[0x2b] /=0x2
0d 01 2b 06 ; all[0x2b] -=0x6
21 02 2b 16 ; if all[0x2b] != all[0x16]
1f 01 5c ; cmd +=0x5c

17 02 2c 19 ; all[0x2c] +=all[0x19]
0e 02 2c 18 ; all[0x2c] -=all[0x18]
22 01 2c 05 ; if all[0x2c] !=0x5
20 01 4d ; cmd +=0x4d

18 02 2d 19 ; all[0x2d] +=all[0x19]
0f 02 2d 15 ; all[0x2d] -=all[0x15]
23 01 2d 0b ; if all[0x2d] !=0xb
21 01 3e ; cmd +=0x3e

04 01 2a 02 ; all[0x2a] *=0x2
04 01 2a 02 ; all[0x2a] /=0x2


// 下面是输出部分，从0到0x1a输出内容，如果执行正确，应该会执行到这里
04 00 04 01 04 02 04 03 04 04 04 05 04 06 04 07 04 
08 04 09 04 0a 04 0b 04 0c 04 0d 04 0e 04 0f 04 
10 04 11 04 12 04 13 04 14 04 15 04 16 04 17 04 
18 04 19 04 1a

解题脚本

根据上面的约束，直接写到z3里面即可。我这里写的太啰嗦了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
from z3 import *



def to_int(x):
    return ArithRef(Z3_mk_bv2int(x.ctx_ref(), x.as_ast(), 0), x.ctx)

def solve():
    f5 = BitVec("f5",8)
    f6 = BitVec("f6",8)
    f7 = BitVec("f7",8)
    f8 = BitVec("f8",8)
    f9 = BitVec("f9",8)
    fa = BitVec("fa",8)
    fb = BitVec("fb",8)
    fc = BitVec("fc",8)

    fd = BitVec("fd",8)
    fe = BitVec("fe",8)
    ff = BitVec("ff",8)
    f10 = BitVec("f10",8)
    f11 = BitVec("f11",8)
    f12 = BitVec("f12",8)
    f13 = BitVec("f13",8)
    f14 = BitVec("f14",8)
    f15 = BitVec("f15",8)
    f16 = BitVec("f16",8)
    f17 = BitVec("f17",8)
    f18 = BitVec("f18",8)
    f19 = BitVec("f19",8)
    solver = Solver()
    solver.add(f5+f7 == 0xcc)
    solver.add(f5+f6+f7-0x64==0xe1)
    solver.add(f6+f7 == 0xd8)
    solver.add(f8==f9+0xb)
    solver.add(f8==fa+0x42)
    solver.add(fc + fb - f8 == 0x67)
    solver.add(fc+fa-f9 == fb-0x29)
    solver.add(fb-fa == 0x35)

    solver.add(fe == f13)
    solver.add(ff == f12)
    solver.add(f10 == f7)
    solver.add(fd-f12==f11)
    solver.add(f11<f12)
    solver.add(f11>f13)
    solver.add(fd-0x36 == fe)
    solver.add(f12-f13==2)

    
    solver.add(2*f13==f17)
    solver.add(f14==f10)
    solver.add((f15/2)  == f16 + 0x6)
    solver.add((f15/2)*2 == f15)
    solver.add(f16==fa)
    solver.add(f19-f18 == 0x5)
    solver.add(f19-f15 == 0xb)
    if solver.check() == z3.sat:
        print("can solve")
        m = solver.model()
        # a5 = int(str(m.evaluete(f5)))
        a5 = m[f5].as_long()
        a6 = m[f6].as_long()
        a7 = m[f7].as_long()
        a8 = m[f8].as_long()
        a9 = m[f9].as_long()
        aa = m[fa].as_long()
        ab = m[fb].as_long()
        ac = m[fc].as_long()
        ad = m[fd].as_long()
        ae = m[fe].as_long()
        af = m[ff].as_long()
        a10 = m[f10].as_long()
        a11 = m[f11].as_long()
        a12 = m[f12].as_long()
        a13 = m[f13].as_long()
        a14 = m[f14].as_long()
        a15 = m[f15].as_long()
        a16 = m[f16].as_long()
        a17 = m[f17].as_long()
        a18 = m[f18].as_long()
        a19 = m[f19].as_long()
        ans = ""
        ans +=chr(a5)
        ans +=chr(a6)
        ans +=chr(a7)
        ans +=chr(a8)
        ans +=chr(a9)
        ans +=chr(aa)
        ans +=chr(ab)
        ans +=chr(ac)
        ans +=chr(ad)
        ans +=chr(ae)
        ans +=chr(af)
        ans +=chr(a10)
        ans +=chr(a11)
        ans +=chr(a12)
        ans +=chr(a13)
        ans +=chr(a14)
        ans +=chr(a15)
        ans +=chr(a16)
        ans +=chr(a17)
        ans +=chr(a18)
        ans +=chr(a19)
        print(ans)
    else:
        print("can't solve")

if __name__ == "__main__":
    solve()

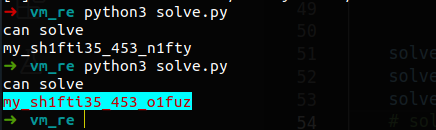
image-20220415171305002

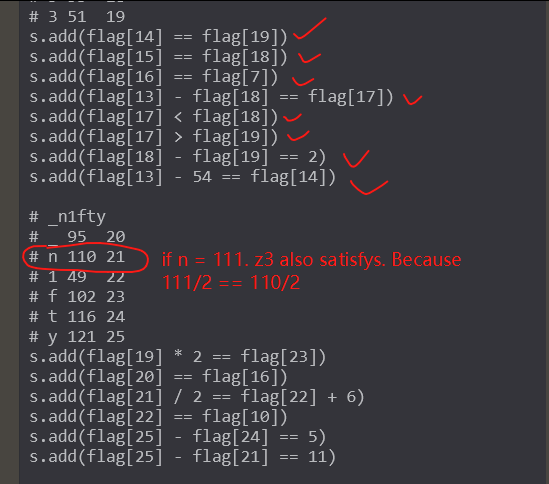
多解问题

注意到上面有一个除法操作。这里会产生多解问题。

unknown

这样会产生两种可能的解。

  1. flag{my_sh1fti35_453_n1fty}
  2. flag{my_sh1fti35_453_o1fuz}

后面询问了出题人，两种都算是可以了。

本文标题:hackpark2022_shiftycode

文章作者:

发布时间:2022-04-15, 15:31:35

最后更新:2022-04-17, 12:02:06

原始链接:https://nicholas-wei.github.io/2022/04/15/hackpark2022-shiftycode/

许可协议: "署名-非商用-相同方式共享 4.0" 转载请保留原文链接及作者。

文章目录
  1. 1. 简单逆向
    1. 1.1. 输出
    2. 1.2. 整体逻辑
    3. 1.3. 解题脚本
    4. 1.4. 多解问题
|